كيفية تمثيل وترميز الصوت في الحاسوب
كيف يفهم ويخزن الحاسوب مقاطع الصوت والموسيقى
لنتعرف قليلًا (وبشكل سريع) على بعض الأمور الخاصة بالصوت لفهم كيف يتم حفظه في الحاسوب.
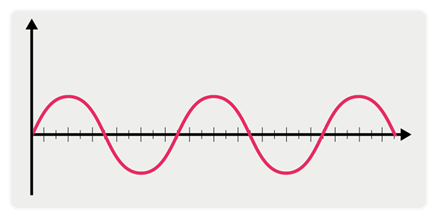
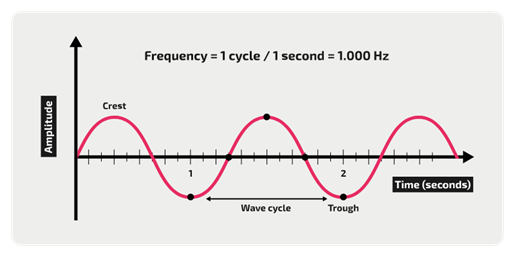
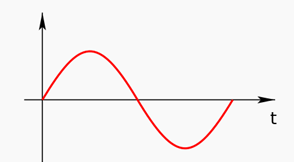
الصوت هو عبارة عن اهتزازات، وتدعى الأمواج الصوتية، ويتم تمثيلها على محور الإحداثيات بمنحني يشبه التالي:
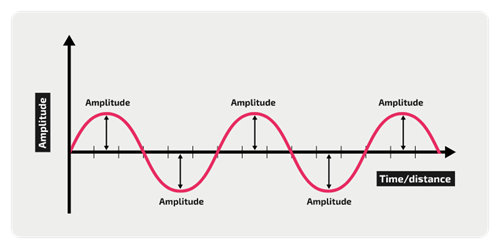
يكون لذلك المنحني عدة خواص، الأولى السعة وتدعى amplitude وهو بُعد المنحني عن محور الإكسات، وزيادته يعني علو (ارتفاع) الصوت:
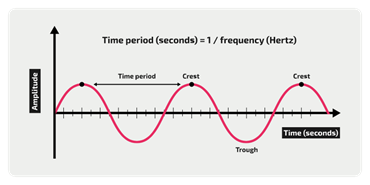
يكون لكل موجة نمط متكرر، والتكرار الواحد للموجة يدعى دورة (cycle) أو تواتر (frequemcy). والمدة الزمنية هي الزمن المطلوب لإكمال دورة واحدة. وهذا يعني على المخطط المسافة بين أعلى أو أخفض نقطتين متتابعتين للمنحني:
وتُحسب المدة الزمنية تلك وفق القانون: 1/التواتر. أي مقلوب التواتر. ولكن ماهو التواتر بالضبط؟
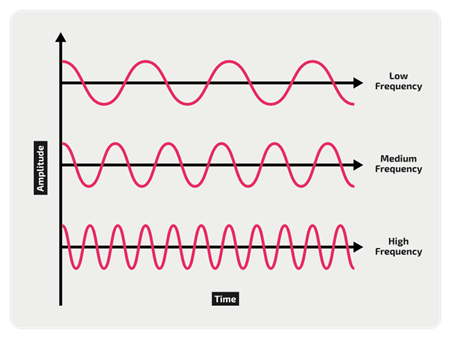
التواتر هو عدد دورات الموجة الصوتية في الثانية. تُظهر الصورة التالية من الأعلى للأسفل: تواتر منخفض – متوسط – عالي:
التواتر العالي يعني أن الصوت رفيعًا أكثر. أي أن تواتر الموجات الصوتية لصوت الفتيات أعلى من تواتره لصوت الشبان. ويُحسب التواتر بتقسيم عدد الدوارت على الزمن، فإذا كان للموجة الصوتية دورة واحدة في الثانية مثلا، فيكون تواترها 1 هرتز Hz، وإذا كانت الموجة تكرر نفسها 10 مرات في الثانية فيكون تواترها 10 هرتز، وهكذا.
يمكن للأذن البشرية سماع الأصوات التي تكون تواتر موجاتها بين 20 إلى 20 ألف هرتز تقريبًا (ويضيق هذا المجال مع التقدم في السن). يمكن الاطلاع على المقطع القصير التالي الذي يعرض تواتر الصوت (مرئيًا وصوتيًا). شغل المقطع وحدد التواتر الذي بدأت بالسماع عنده، والتواتر الذي فقدت القدرة على السماع عنده. هل تعتقد أنك هرمت مثلي؟: https://www.youtube.com/watch?v=qNf9nzvnd1k
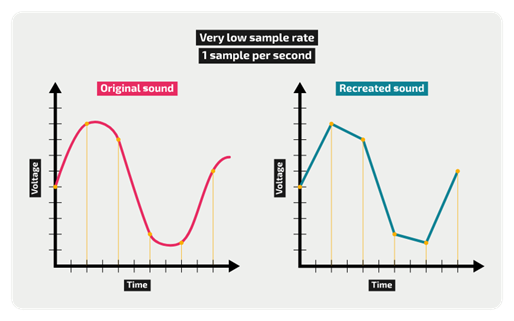
الحقيقة أنك ستسمع منذ أول ثانية في المقطع في حال وضعت سماعات جيدة، وطبعًا في حال لم تكن شيخًا عجوزًا. ولكن لا تجرب ذلك كثيرًا وترفع الصوت كي لا تفقد أو تضر بسمعك. ونأتي الآن للمهم، كيف يمكن تمثيل تلك الموجات الصوتية في الحاسوب؟ أي تحويلها لأصفار وواحدات؟ يتم عبر أخذ عينات (sampling) من المنحني في كل فترة زمنية معينة. تُظهر الصورة على اليسار الموجة الأصلية وعلى اليمين العينات المأخوذة في كل ثانية:
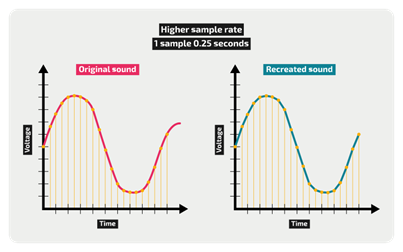
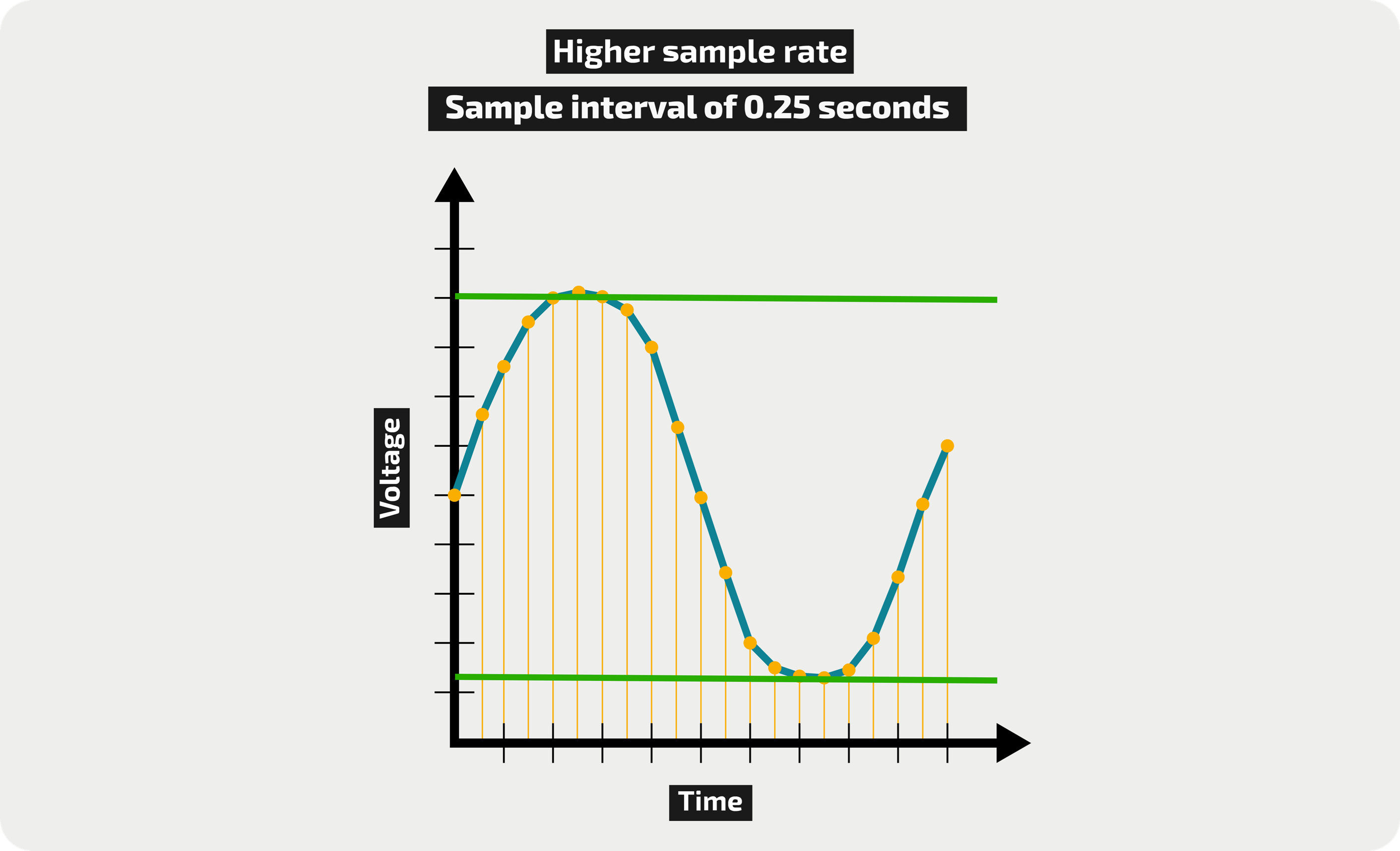
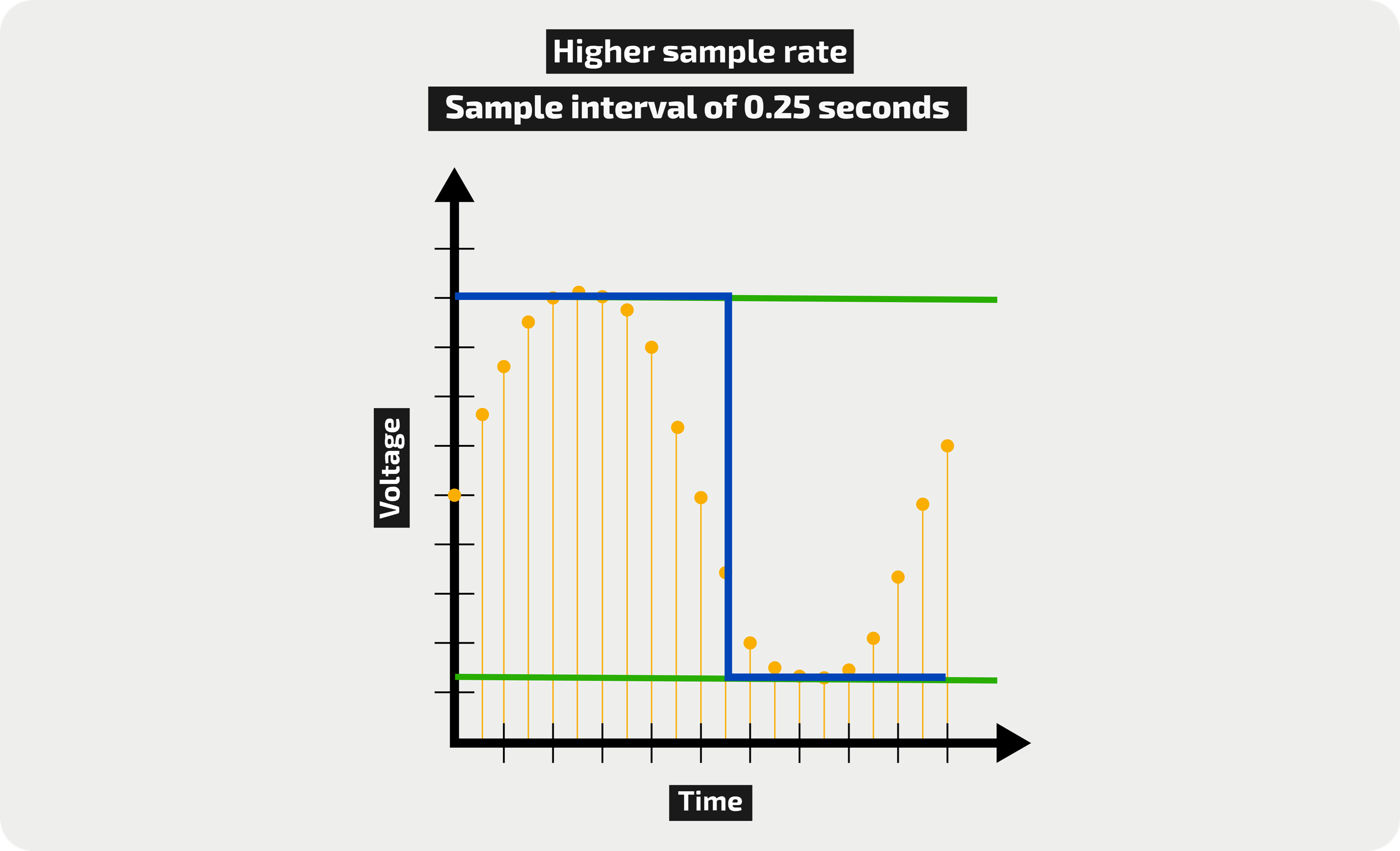
كلما قلّت الفترة الزمينة، أي كلما ازدادت العينات تلك ازداد معدل تشابه الصوت المسجل مع الصوت الأصلي، الصورة التالية تُظهر أخذ عينة (sample) كل ربع ثانية:
ولكن ماهي تلك العينات؟ هل تعتقد أنه من الجيد تسجيل بت واحد كل فترة زمنية معينة؟ أي جعل العينة عبارة عن بت يحمل قيمة 0 أو 1، هل سيكون ذلك جيدًا؟ البت الواحد سيتمكن من حمل قيمتين مختلفتين، وبالتالي يمكن أن يسجل نقطتين فقط على المحور العامودي Y، انظر الخطان بالأخضر:
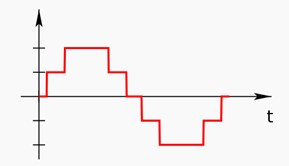
وهذا يعني أن المنحني لن يتم تمثيله فعليا كما هو ظاهر في الصورة، وإنما كل نقطة مأخوذة منه ستحمل إحدى القيمتين، إما في الأعلى أو في الأسفل. أي سيكون المنحني فعليا يشبه الشكل التالي (الخط الأزرق)، حيث يتم تقريب كل نقطة إما للأعلى أو للأسفل (للمستويَين الذين يمكن تمثيلهما في بت واحد):
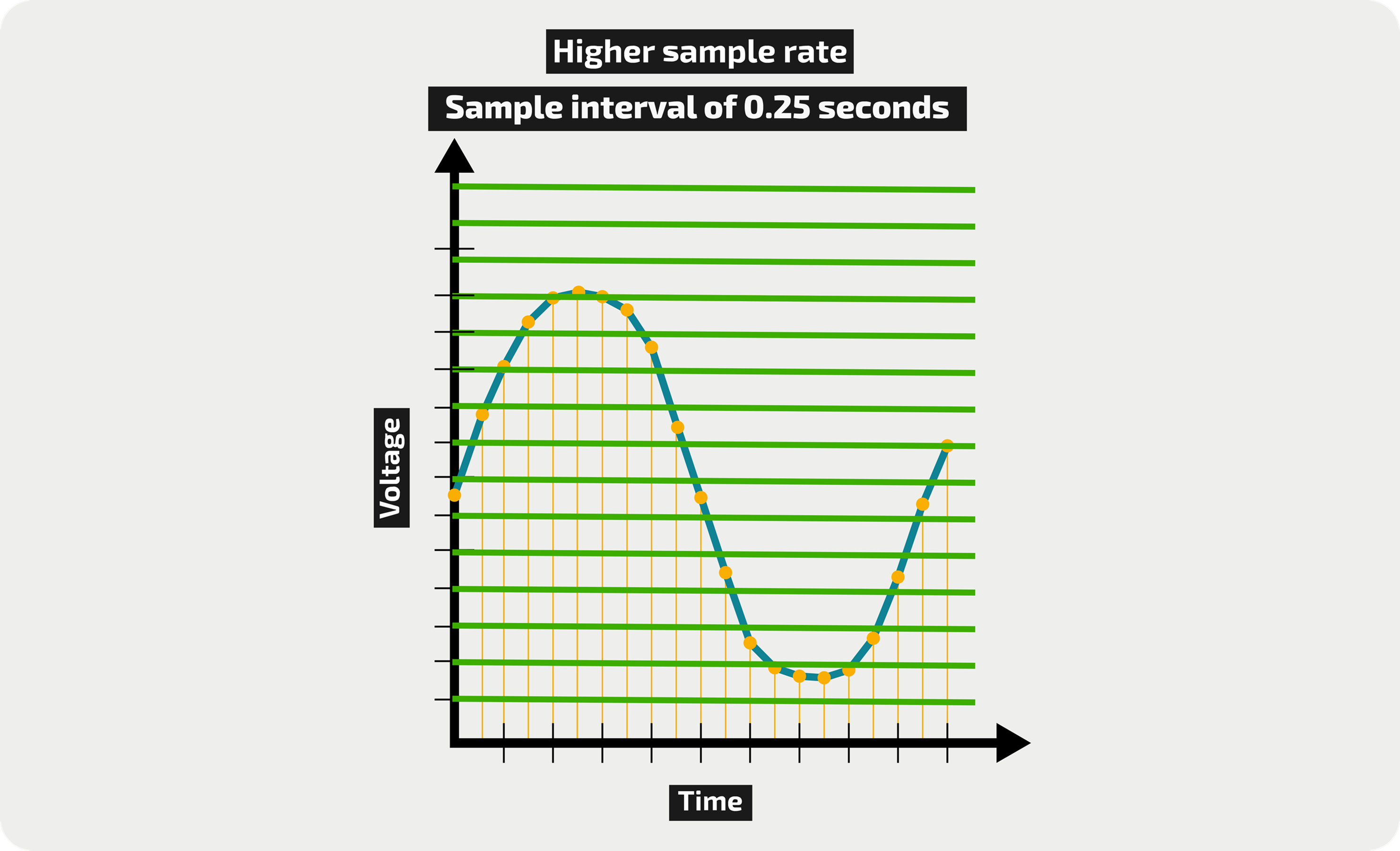
طبعا الجزء الشاقولي من الخط الأزرق لا يتم تمثيله، وكان الأصح عدم عرضه في الصورة. إذًا يجب استخدام أكثر من بت أليس كذلك؟ كل بت إضافي يعني قيمتين إضافيتين. باستخدام 4 بت مثلا سيكون لدينا 24 أي 16 مستوى مختلف على محور الـ Y. وهذا أفضل بلا شك:
الفترة الزمنية المحددة التي يتم أخذ العينات عند مرورها تدعى sample interval أي مجال العينة وتمثل النقاط على المحور الأفقي X، وتكون تلك الفترة أو المجال عادة صغير جدا، بحيث يتم أخذ 44100 عينة في الثانية! ( 44100 هرتز؛ معدل تواتر العينات) أما عدد البتات عند كل عينة فيمثل المستويات على المحور العامودي Y ويكون عادة 16 بت (2 بايت) وهذا يعني 216 أي 65536 مستوى مختلف على محور Y. وهذا يعطي عموما دقة صوت عالية.
لقد قلت لك أن الإنسان عموما يسمع لغاية تواتر (frequency) يساوي 20 ألف هرتز، فلماذا يكون تواتر التسجيل إذًا 44100 أي أكثر من الضعف؟!
ادّعى شخص يُدعى هاري (Harry Nyquist) عام 1928 أننا لنتمكن من إنتاج تسجيل صوتي بدقة عالية، فيجب على الأقل استخدام معدل عينات (تواتر عينات) أكثر من ضعف أعلى تواتر للصوت الأصلي. وقد تم إثبات تلك النظرية من قبل Claude Shannon عام 1949. لذا فمعدل العينات المستخدم (44100) هو أكثر من ضعف أعلى تواتر يمكن أن يلحظه الإنسان.
يوجد تفاصيل أكثر عن الصوتيات وتسجيلها وضغطها لم نذكرها هنا، فهدف هذه الفقرة هو إعطاء نبذة سريعة عن الموضوع لا أكثر.
مرجع هذه الفقرة:
وقد أُعطيت الرخصة التالية لاستخدامه:
https://www.nationalarchives.gov.uk/doc/open-government-licence/version/3/
بقي أن أقول لك أن الإشارة التي تمثل الموجات الصوتية قبل تمثيلها تدعى الإشارة التماثلية analog singal وتكون مستمرة وتحوي قيم متغيرة مع الزمن، أما الإشارة التي نتجت بعد أخذ العينات والترميز في النظام الثنائي تدعى الإشارة الرقمية digital signal، وهي لا يمكن أبدًا أن تصل لدقة الإشارة الأصل، ولكنها تصل لدقة كافية.
الإشارة الرقمية والإشارة التماثلية
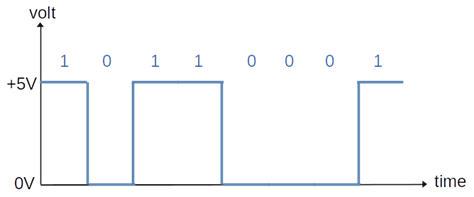
أحد الطرق الفعلية لنقل البايتات (صفر أو واحد) كهربائيًا عبر الأسلاك النحاسية، هو تمثيل الواحد بـ +5 فولت والصفر بـ 0 فولت. وبالتالي إذا أردنا نقل العدد 177، والذي يكون في النظام الثنائي 10110001، فسيكون كهربائيًا بالشكل الظاهر بالمخطط التالي، حيث يمثل المحور الأفقي (محور X) الزمن، والمحور العامودي (المحور Y) شدة التيار:
ولكن كم هي المدة الزمنية الفعلية بين بت وآخر؟ أي كم هي مدة كل خط أفقي نراه في المخطط؟
يختلف بحسب معدل البتات في الثانية (bit rate) والذي يختلف بدوره بحسب الأداة المستخدمة للتواصل، فإذا كنا نتحدث مثلا عن الكبل الذي يصل بين الحاسوب والمودم، وهو كبل Ethernet، والنواع الأكثر شيوعًا منه اليوم هو 100BASE-TX حيث يمكن أن يعطي سرعة 100Mbps أي مئة ميغا بت في الثانية، والميغابت هو مليون بت، وبالتالي بتطبيق القانون التالي نحصل على المدة الزمنية بين بت وآخر:
period = 1 / bit rate = 1 / 1 000,000,000 = 0.00000001 seconds = 10 nanoseconds
ويمسى bit rate كذلك بـ baud rate. وواحدته بت في الثانية bit per second أو اختصارًا bps
أما بالنسبة ﻷجهزة الوايفاي، والأكثر شيوعًا اليوم هي التي تستخدم معيار 802.11n حيث تتراوح السرعة فيها بين 54 Mbps إلى 600 Mbps، وذلك حسب البعد وتداخل الإشارات مع بعضها وحالة الشبكة. فإذا افترضنا أن السرعة هي 150 Mbps فتكون المسافة الزمنية بين البت والآخر هي:
Period = 1 / 150,000,000 = 0.00000000667 seconds ≈ 6.67 nanoseconds.
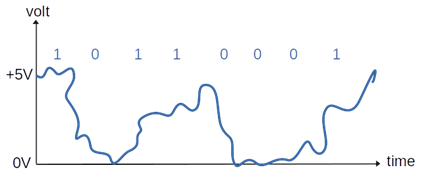
ولكن الإشارات فعليًا لا تصل بالشكل الموضح أعلاه (سواء السلكية أو اللاسلكية)، فلا يوجد مثالية في الحياة، وإنما تصل الإشارة بسبب المسافة والتشويش والتداخلات بشكل يشبه الشكل التالي (التشويش يحدث في الأسلاك أيضًا وليس فقط في التواصل اللاسلكي):
ولكن لا يسبب ذلك مشكلة، ﻷننا نعلم أن كل قيمة لا يمكن أن تكون سوى إحدى حالتين، إما 5 فولت أو صفر فولت، وبالتالي يتم التقريب، فإذا كان التيار أقرب لـ 5V يُحسب على أنه كذلك، أي 1 في العد الثنائي، وإذا كان أقرب للصفر يُحسب على أنه صفر.
يتم تمثيل الإشارات في الحياة، سواءً الإشارات اللاسلكية (أمواج الراديو الكهرومغنطيسية) أو أمواج الصوت، بالإشارة التماثلية وتسمى Analog signal وتكون بالشكل التالي:
حيث تحمل قيمة متغيرة مع الزمن، بينما تكون الإشارة الرقمية لها بالشكل التالي، وهي تقاربها ولكن لا يمكن أن تصل لدقتها (لا يمكن أن تعطي القيمة الفعلية للإشارة الأصل في كل لحظة):
بما أن قيم الإشارة التماثلية تكون متصلة، بحيث يكون لكل لحظة قيمة مختلفة، فيمكن التفكير على أن قيم مفتاح تغيير معدل الصوت متصلة وتماثلية:
ﻷننا يمكننا وضع ذلك المفتاح على أي قيمة. فإذا كانت القيم المتاحة بين 0 و 10 مثلا، يمكن أن نحصل على مستوى الصوت 2.4123 عبر تدوير المفتاح ببطئ ودقة. بينما إذا أردنا تغيير الصوت بشكل رقمي فيجب إعطاء قيم متقطعة، مثل المستوى 1 والمستوى 2 ..إلخ. أو يمكن زيادة الدقة عبر زيادة عدد البتات لكل مستوى (كما في ترميز الصوت) بحيث نشمل رقم واحد مثلا بعد الفاصلة، لنتمكن من الحصول على المستوى 2.1 و 2.2 إلخ. ولكن المستوى الرقمي، أي تغيير الصوت رقميًا لن يعطى أبدًا الدقة التي يعطيها الزر الذي يعطي قيم متصلة غير متقطعة. ومن هنا نعلم معنى كلمة “متقطعة”. وقد وُضع علم كامل بهذا الخصوص يسمى “الرياضيات المتقطعة” وبالإنجليزية Discrete mathematics وهي مادة يدرسها طلاب علم الحاسوب، وقد تجدها على هذه المنصة في وقت ما.