العمليات الحسابية على اﻷعداد الثنائية
العمليات على الأعداد في نظام العد الثنائي وكيفية تمثيل الأعداد السالبة وتمثيل الفاصلة عبر الإزاحة
تعلمنا في الدرس السابق أنظمة العد وطرق التحويل بينها. ولنتعلم الآن كيفية إجراء العمليات الحسابية وتمثيل الأعداد السالبة وكذلك تمثيل الفاصلة في الأعداد الثنائية.
جمع وطرح الأعداد الثنائية
لنتعلم كيفية جمع وطرح الأعداد الثنائية عبر المقطع التالي:
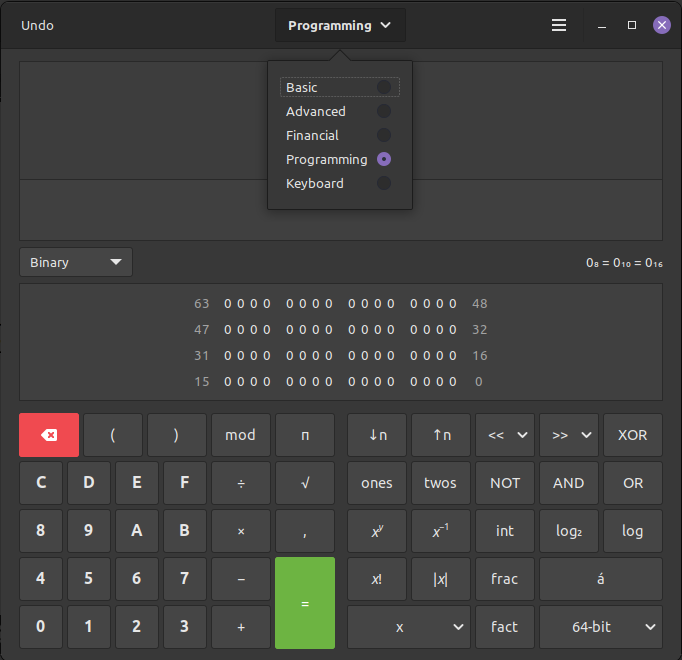
هل تعلم؟ يمكن استخدام الآلة الحاسبة في نظام تشغيل الحاسوب لديك (ويندوز أو لينكس أو ماك) لإجراء العمليات الحسابية في أنظمة العد الأربعة التي تعلمناها. ابحث في إعدادات الآلة الحاسبة عن خيار المبرمج programming أو ماشابه. الصورة التالي لضبط ذلك في الآلة الحاسبة الافتراضية في نظام التشغيل لينكس منت.
تمرين
(حلول التمارين في آخر الصفحة)
أ. ماهو العدد الثنائي الناتج من عملية الطرح التالية في النظام الثنائي:
\[1110 – 101\]تمثيل الأعداد السالبة في نظام العد الثنائي
نعلم أننا في نظام العد العشري نضع السابقة (-) قبل العدد لتمثيل العدد السالب. ولكن لا يمكن في النظام الثنائي (في ذاكرة الحاسوب) وضع سوابق ورموز، وإنما فقط صفر أو واحد (تيار أو انعدام تيار). لذا يجب التفكير بطريقة للتمكن من تمثيل الأعداد السالبة في النظام الثنائي.
هنا قام العلماء بالتفكير، وقالوا لأنفسهم لماذا لا نضيف بِت (bit) إضافي على يسار العدد، بحيث يكون ذلك البت صفرًا إذا كان العدد موجبًا وواحدًا إذا كان العدد سالبًا (وأطلقوا عليه اسم sign bit أي بت الإشارة). فمثلًا إذا كان لدينا مساحة لـ 8 بت، فيكون العدد 1 بالشكل 00000001 والعدد -1 بالشكل 10000001. أليست هذه فكرة جيدة؟
ليس تمامًا! أولًا يصبح للعدد صفر تمثيلان، ناقص صفر 00000000 وزائد صفر 10000000. كما يتطلب الجمع والطرح سلوك مختلف بناءً على بِت الإشارة ذاك. استُخدمت هذه الطريقة في الأجهزة الأولى من الحواسيب مثل IBM 7090، ولم تُستخدم لاحقًا، حيث تم اقتراح طريقة المتمم الأحادي.
المتمم الأحادي Ones’ complement
يتم الحصول على المتمم الأحادي لأي عدد ثنائي بقلب جميع الأصفار لواحدات وجميع الواحدات ﻷصفار (قلب الأرقام يعني في الحاسوب تطبيق العملية المنطقية NOT عليها). وسمي بالمتمم الأحادي ﻷن حاصل جمع العدد مع متممه الأحادي يُنتج عددًا كله واحدات (جرب ذلك بنفسك).
المتمم الأحادي هو أحد طرق تمثيل الأعداد السالبة في نظام العد الثنائي، حيث يمثل المتتم الأحادي لأي عدد (موجب) العدد السالب له.
يتم في الحاسوب دائمًا إعطاء مساحة محددة من الذاكرة لكل نوع من الأعداد.
تعطي مثلًا معظم لغات البرمجة 32 بت للأعداد الصحيحة (integers). ويتم التفريق في الكثير من لغات البرمجة أيضًا بين نوعي الأعداد signed و unsigned وتعني بإشارة (موجب وسالب) أو بدون إشارة (موجب فقط)..ولكن ماذا يعني هذا؟
إذا أردنا تمثيل الأعداد السالبة والموجبة معًا فسنحتاج دائمًا إلى بت إضافي (أول بت على اليسار ويدعى most significant bit و Msb اختصارًا) لتحديد فيما إذا كان العدد موجبًا أو سالبًا، حيث يكون ذلك البت 1 في الأعداد السالبة و 0 في الأعداد الموجبة (نعم كما في الطريقة السابقة ولكن بقلب الأرقام كلها كما ذكرنا).
مثال: لننظر كيف يمكن تمثيل الأعداد من -7 لـ +7، وكما تعلم، العدد +7 هو 111 في النظام العشري، لذا سنتطلب بت رابع لتمثيل الأعداد السالبة ضمن هذا المجال (تكون المساحة المخصصة عمومًا من مضاعفات العدد 2، أي 4 بت، 8 بت، 16 بت، 32 بت..الخ. وهذا مهم لنجاح تمثيل الأعداد السالبة. ستحصل على نتائج خاطئة إذا جربت تمثيل الأعداد السالبة على خمس خانات مثلًا وإجراء العمليات عليها).
| العدد العشري | العدد الثنائي الموجب | العدد الثنائي السالب |
|---|---|---|
| 0 | 0000 | 1111 |
| 1 | 0001 | 1110 |
| 2 | 0010 | 1101 |
| 3 | 0011 | 1100 |
| 4 | 0100 | 1011 |
| 5 | 0101 | 1010 |
| 6 | 0110 | 1001 |
| 7 | 0111 | 1000 |
لاحظ كيف أن أول بت على اليسار دائمًا صفر في الأعداد الموجبة ودائمًا واحد في الأعداد السالبة. وهكذا يتم التفريق بين السالب والموجب. ولذلك السبب إذا قلت لك أننا نريد تمثيل الأعداد ضمن مساحة 4 بت فقط، وسألتك عن أكبر عدد يمكن تمثيله في تلك المساحة، فستسألني: هل تريد تمثيل الأعداد الموجبة فقط (unsigned) أم الموجبة والسالبة (signed)؟ فإذا كان الموجبة فقط، فلن تخصص بت للإشارة وستستخدم كل البتات لديك، وبالتالي يكون أكبر عدد هو 1111 أي 15 وستقول لي حينها أننا يمكننا تمثيل الأعداد من 0 لـ 15. أما إذا أردت الأعداد الموجبة والسالبة فستخصص البت على اليسار للإشارة وينتج لديك 3 بتات فقط يكون فيهم أقصى قيمة هي 111 أي 7 كما في الجدول أعلاه وسنتمكن من تمثيل الأعداد من -7 لـ +7.
لقد طرحنا سؤال في الفقرة السابقة لم نجب عنه، وهو طرح عدد من عدد أصغر منه في النظام الثنائي، حيث رأينا كيف أننا نستعير واحد من العدد المجاور للصفر، ولكن في هذه الحالة لن يوجد واحد لنستعيره، فكيف نجري عملية الطرح تلك؟ لنرى:
ملاحظة:: لا تنس أننا نعتبر البت الأول من اليسار لتمثيل العدد الموجب والسالب فقط في حال علمنا أن الأعداد تحوي موجبًا وسالبًا، وإلا فلا يمكننا فرض ذلك وقد يكون العدد موجب حتى لو كان أول رقم فيه هو 1.
لاحظ أن للصفر تمثيلان في هذه الطريقة! صفر سالب وصفر موجب كما هو موضح في الجدول المبين أعلاه. رغم أننا نعلم أن الصفر ليس له إشارة (ليس لها معنى مع الصفر)، وبالتالي يشكل هذا عيب واضح في طريقة تمثيل الأعداد السالبة هذه. رغم أن الجمع والطرح مع الصفر السالب سيعطي نفس العدد، أي لا يوجد مشكلة حسابية في ذلك. ومع هذا يبقى وجود تمثيلان للصفر يسبب مشكلة ويوجب اختبار البرمجيات للصفر السالب أيضًا في حال استخدامه (إرجاع دالة للصفر أمر شائع جدًا جدًا في كل لغات البرمجة الشهيرة، ووجود قيمتين للصفر يصعِّب عملية التحقق من الصفر). بالإضافة للعيب الآخر الذي شاهدناه في الخطوة الإضافية التي تتطلبها في الجمع والطرح.
تم حل هذه المشاكل في الطريقة المستخدمة في حواسيب اليوم. وهي المتمم الثنائي.
المتمم الثنائي Two’s complement
يَستخدم المتمم الثنائي أول بت يسارًا _كما في السابق_ للتفريق بين العدد السالب والموجب. ويتم تحويل العدد إلى متتمه الثنائي عبر التحويل أولًا للمتمم الأحادي ثم إضافة 1 (الجمع مع 1). لاشيء آخر.
فمثلًا يكون العدد +6 في النظام الثنائي بالشكل 0110، نحول للمتمم الأحادي بقلب الواحدات أصفارًا والأصفار واحدات فينتج 1001. نضيف الآن واحدًا:
0001
----
1010
ويكون بذلك العدد 1010 (الذي يعبر عن -6 وفق هذه الطريقة) المتمم الثنائي للعدد 0110.
لاحظ مجددًا أول بت من اليسار كيف أنه صفر في الموجب وواحد في السالب.
ولكن مافائدة إضافة الواحد؟
هذه العملية الإضافية البسيطة التي تشكل الفرق بين هذه الطريقة وطريقة المتمم الأحادي هي التي تحل المشكلتين المذكورتين أعلاه. أولًا، يصبح للصفر تمثيلًا واحدًا. ففي مساحة 4 بت يكون الصفر 0000، نحوله للمتمم الأحادي فيصبح 1111 ونضيف واحدًا له، ليعود 0000 (ولا يوجد مساحة إضافية للواحد الزائدة – وهذا مايسمى تجاوز السعة overflow وهو أمر جيد ومطلوب هنا؛ أي تجاهل الواحد الزائدة). ولكن مالذي يمثله 1111 في هذه الطريقة؟ إنه يمثل العدد -1، كيف؟ لنأخذ +1 والذي يكون في مساحة 4 بت بالشكل 0001، لنحوله للمتمم الأحادي 1110 ثم نضيف واحد فيصبح 1111.
أما المشكلة الثانية وهي الخطوة الإضافية التي كانت مطلوبة في الجمع والطرح لم تعد مطلوبة هنا وصار بإمكاننا التعامل مع الأعداد السالبة مثل أي عدد ثنائي، فيمكن تحويله مباشرة للنظام العشري بنفس الطريقة التي تعلمناها، وذلك عبر ضرب كل رقم بـ 2 مرفوعًا ﻷس الخانة. لنجرب ذلك مع العدد -6 الذي ذكرناه قبل قليل، وهو 1010:
نعم كما لاحظت، الفرق فقط في أننا نضرب أول رقم والذي هو بت الإشارة بـ -2 بدلا من 2، ﻷنه بت الإشارة ببساطة، وهو واحد هنا فهذا يعني أن العدد سالب.
لنرى الأعداد التي يمكن تمثيلها ضمن مساحة 4 بت:
| 0 | 0000 |
| 1 | 0001 |
| 2 | 0010 |
| 3 | 0011 |
| 4 | 0100 |
| 5 | 0101 |
| 6 | 0110 |
| 7 | 0111 |
| -8 | 1000 |
| -7 | 1001 |
| -6 | 1010 |
| -5 | 1011 |
| -4 | 1100 |
| -3 | 1101 |
| -2 | 1110 |
| -1 | 1111 |
لاحظ أنه يمكننا تحويل العدد من المتمم الثنائي، أو من السالب للموجب عبر قلب الواحدات والأصفار وإضافة واحد (وهذه نفس العملية!)، فالعدد 1011 إذا قلبناه 0100 وأضفنا واحدًا ينتج 0101 وهذا هو الرقم 5.
هل يوجد مشاكل في هذه الطريقة المستخدمة اليوم؟
هل لاحظت كيف حللنا مشكلة تمثيلي الصفر؟ وذلك عبر تجاهل تجاوز السعة، أي عندما لا يوجد سعة كافية فعليًا للواحد المضافة، وبذلك فقط نحصل على المطلوب، ولكن ماذا لو وُجد سعة؟! لنجري العملية مجددًا، حيث لدينا مثلًا العدد صفر بالشكل 0000 ونقلبه للمتمم الأحادي 1111 ثم نضيف واحد (مع وجود سعة لبت إضافي) فسيصبح الناتج 10000، وهذا ليس صفرًا، وبالتالي في هذه الحالة سيكون الناتج غير المتوقع والمطلوب.
لذا يجب في هذه الطريقة تحديد المساحة ومنع العدد من تجاوز تلك المساحة وأخذ بت إضافي عن المعطى له في البداية.
حل مشكلة وجود تمثيلين للرقم صفر يؤدي للتالي: لا يمكن تمثيل العدد الموجب ﻷصغر عدد سالب.
يعني إذا كان لدينا مساحة ثمانية بت، وبتخصيص بت للإشارة يبقى 7 بت، يكون أكبر عدد (موجب) يمكن تمثيله هو 01111111 ( \(127_{dec}\) ) ولا يمكن أبدًا تمثيل 128 في هذه المساحة، في حين يكون العدد 10000000 هو -128، وبالتالي مجال الأعداد الذي يمكن تمثيله في مساحة ثمانية بت ووفق طريقة المتمم الثنائي هو +127 و -128. ويكون وفق أي مساحة معطاة استحالة تمثيل العدد الموجب ﻷصغر عدد سالب.
إذا نظرنا للمتمم الثنائي للعدد -128 في مساحة 8 بت فسيكون الناتج هو نفسه:
| -128 | $1000 0000$ |
| المتمم الأحادي | $0111 \quad 1111$ |
| المتمم الثنائي | $1000 \quad 0000$ |
رغم أن سالب العدد السالب (128-)- يجب أن يعطي عددًا موجبا +128، ولكن الحال ليس كذلك كما رأيت. وقد يقود هذا أيضًا لعدة مشاكل في البرمجة (فيما يتعلق بأصغر عدد سالب):
-
ماذكرناه للتو، وهو الخطأ:
\[-(-128) = -128\]وهذا الخطأ ينطبق على الضرب بـ -1
- إعطاء عدد سالب لناتج القيمة المطلقة: \(|-128| = -128\)
- قد يؤدي التقسيم على -1 لخطأ (مثل التقسيم على صفر حيث يكون غير معرف).
تسري الأخطاء التالية على لغات معروفة اليوم مثل C و ++C، فقد تُحدث العمليات أعلاه نتائج غير متوقعة. وهي وظيفة المبرمج الجيد أن يكون على دراية بهذه الأمور ويتجنب إجراء العمليات هذه بشكل مباشر.
لماذا يدعى المتمم الثنائي؟
ﻷن جمع العدد مع متممه الثنائي سيُعطي دائمًا \(2^N\) حيث تعبر N عن المساحة المعطاة للعدد. فمثلًا إذا كان N=3 أي لدينا مساحة لـ 3 بت، فيكون مجموع أي عدد مع متممه الثنائي هو \(2^3\) أي 8. يمكن ضمن تلك المساحة وﻷخذ مثال، تمثيل الرقم \(3_{dec}\) حيث يتطلب بِتّان والبت الثالث للإشارة، ويكون 011، متتمه الأحادي 100 مضافا له واحد نحصل على متممه الثنائي 101، بجمعهم مع بعض:
101
------
1000 = 23 = 8
ربما تقول لي: ولكننا تجاوزنا المساحة عند الجمع!
طبعًا المقصود هنا أن الجمع العادي مع أخذ تجاوز السعة بعين الاعتبار فيكون الناتج كما ذكرنا، إلا أنه في العمليات الحسابية وعند استخدام طريقة المتمم الثنائي يجب عدم السماح بتجاوز السعة، ففي المثال أعلاه قمنا في الواقع بالجمع بين 3 و -3، وعند عدم السماح بتجاوز السعة سيُنتج المطلوب وهو صفر.
لقد قلت لك أن هذه الطريقة هي المستخدمة في حواسيب اليوم، ولكن لا تظن أنها طريقة جديدة تمامًا، فقد تم اقتراحها من قبل John von Neumann منذ عام 1945 واستُخدمت بالفعل في حاسوب EDSAC الصادر عام 1949. ولكن مع هذا فقد استَخدمت معظم الحواسيب آنذاك وحتى الصادرة بعد العام المذكور طريقة المتمم الأحادي، لتهيمن بعد ذلك طريقة المتمم الثنائي على الحواسيب الصادرة من منتصف الستينيات تقريبًا وما بعد.
ولكنك إلى الآن مازلت تقول أن الحاسوب بأكمله يستخدم الطريقة الفلانية، وما علاقة بنية الحاسوب في ذلك؟ ألا يمكن للحاسوب الواحد أن يستخدم أكثر من طريقة لتمثيل الأعداد السالبة؟
سؤال جميل وصعب، لقد تعلمت الآن أن تمثيل الأعداد السالبة وفق طريقة المتمم الثنائي هي الأفضل، كما أنها لا تتطلب خطوة إضافية في الجمع والطرح، وهذا يعني أنه يتم التعامل مع الأعداد السالبة مثل أي عدد آخر دون أي شيء إضافي، وهذا يعني فيزيائيًا أننا نستخدم تمامًا نفس الدارة المنطقية لإجراء الحساب، دون الحاجة لدارة إضافية أو إضافة على دارة الحساب الموجودة. وبالتالي تعتمد معظم الحواسيب الحديثة اليوم في تصميمها الداخلي طريقة المتمم الثنائي، أي أنها موجهة لتستخدم طريقة المتمم الثنائي، وبالتالي يتم استخدام دارة الحساب الرئيسية نفسها دون إضافات.
ومع هذا، قد تتمكن من استخدام تمثيل آخر مثل المتمم الأحادي على جهازك، ولكن سيتطلب ذلك كتابة كود بشكل خاص حتى تتمكن من استخدام الحساب العادي في فهم تمثيل المتمم الأحادي، أي ستتطلب العملية خطوات إضافية وستكون أبطئ قليلًا، كون أن الجهاز نفسه غير مصمم خصيصًا لذلك.
لننظر الآن لجمع الأعداد في حالة اعتبار الأعداد السالبة أيضًا والممثلة وفق طريقة المتمم الثنائي.
جمع الأعداد هنا يتم بشكل طبيعي جدًا وكما تعلمنا، ومع تجاهل أي تجاوز في السعة، أي إذا نتج بت زائد أقصى اليسار فنقوم بتجاهله. مثال:
ولكن هناك مشكلة تجاوز السعة overflow مجددًا، ولكن في حال كان الناتج لا يتسع فعليًا ضمن المساحة المحددة. فإذا كان لدينا مساحة 4 بت، فيمكن تمثيل الأعداد من 7 لـ -8. ولكن إذا أردنا جمع 7 و 3 فهذا سيُنتج العدد 10 والذي لا يمكن تمثيله ضمن 4 بت (على اعتبار البت الأول من اليسار مخصص للإشارة)، كما ترى:
علمًا أن الناتج يكون صحيحًا إذا اعتبرنا العدد unsigned، أي إذا لم نعتبر وجود الإشارة واحتسبنا البت الأول يسارًا. ولكن هذا لا يحدث في حالتنا هنا كوننا نعتبر الأعداد الموجبة والسالبة معًا.
وما حل هذه المشكلة؟
أولًا، يجب أن نحدد وجود المشكلة. وللقيام بذلك لنجيب على السؤال التالي: كيف نعلم أن الناتج خاطئ، أي أن تجاوز في السعة (overflow) قد حصل؟
الأمر بسيط، إذا كان العددان موجبان (البت الأول المخصص للإشارة 0) ونتج عند الجمع عدد سالب (البت الأول 1) فهذا يعني أن المشكلة قد حصلت هنا. كذلك إذا كان العددان سالبان (البت الأول 1) ونتج عند الجمع عدد موجب (البت اﻷول 0) فهذا يعني أن المشكلة قد حصلت. ولا يمكن أن تحدث المشكلة أبدًا عند جمع عدد سالب مع عدد موجب (ﻷن العملية هذه لا يمكن أن تعطي عددًا خارج مجال الأعداد التي يمكن تمثيلها في السعة المحددة).
بعد تحديد المشكلة، يصبح الحل سهلًا، فهو إما إضافة بت إضافي إن كانت الذاكرة تتسع لذلك، أو يمكن إعطاء خطأ للمستخدم. وعمومًا، يبدو أن الحل يختلف بحسب لغة البرمجة المستَخدمة وطريقة تعاملها مع هذه المشكلة.
لننظر لمشكلة تجاوز السعة في لغة سي (ليس من الضروري معرفتك للغة سي هنا، وليس مهما فهم طريقة كتابة الكود في هذا المقطع بل الفكرة، وستتعلم لاحقًا في هذا الكتاب أساسيات لغة سي):
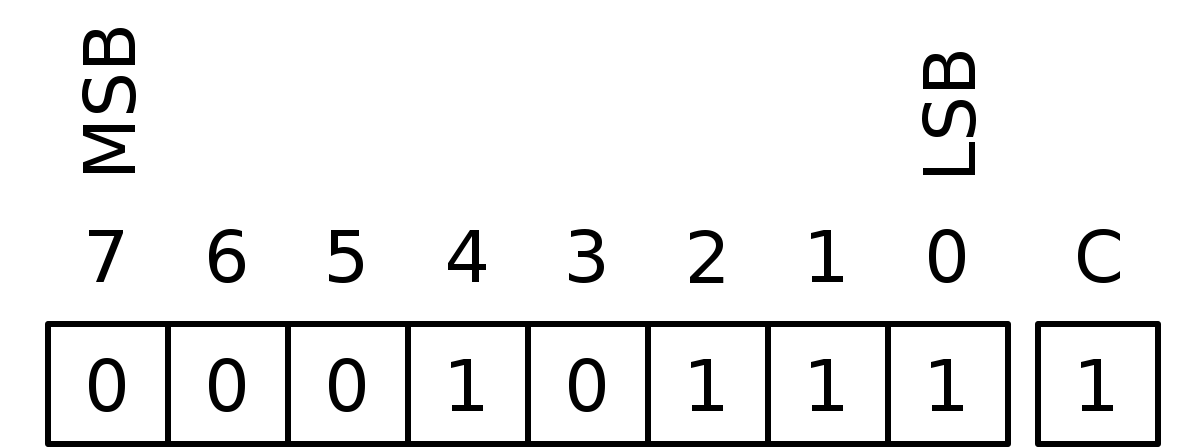
عندما نتحدث عن عمليات الجمع والطرح في الحاسوب، فنحن نتعامل بشكل مباشر مع معالج الحاسوب (CPU) تلك القطعة صغيرة الحجم اليوم والتي تسمى بالعربية وحدة المعالجة المركزية. تحوي تلك المعالجات مساحة 1 بت مخصصة لحفظ الباقي من العملية الحسابية، أو الـ overflow في الحالة التي ذكرناها أخيرًا، ويطلق على تلك المساحة اسم Carry أو Carry Flag. وبالتالي فعندما نجمع عددان ويكون ناتجهما لا يتسع في المساحة المخصصة، أي يزيد 1 بت، يتم حفظ ذلك البت الزائد ولا يضيع. يُظهر الشكل أدناه المساحة المخصصة لحفظ العدد والتي تدعى Register، والبت المخصص لحفظ الباقي أو الزائد وهو Carry كما ذكرنا واختصارا C.
كما لاحظت، فالريجستير أعلاه يحوي 8 بت، لذا فهذا يتعلق بمعالجات الـ 8 بت. أما معالجات اليوم فهي من نوع 64 بت. وسنتحدث بمزيد من التفصيل إن شاء الله عن المعالجات في مقال لاحق إن شاء الله.
تشير MSB في الصورة لـ Most significant bit و LSB لـ Least significant bit يعني أول بت وآخر بت ببساطة.
تتيح بعض لغات البرمجة الوصول لذلك البت المتجاوز لسعة العددين الأصليين والتعامل معه. ولكن لغة سي لا توفر ذلك الوصول لذلك البت (carry bit). لذا يستخدم المبرمجون في لغة سي أنواع المتغيرات التي تعطي ضعف المساحة لحل هذه المشكلة (overflow). فإذا كان المطلوب التعامل مع أعداد لا تتجاوز الـ 32 بت، أي هي نفسها تتسع في 32 بت، ولكننا نعلم أن العمليات الحسابية عليها قد تتجاوز ذلك، فيتم استخدام مساحة 64 بت.
أما عملية الطرح هنا فهي طرح مباشر مع تجاهل تجاوز السعة أيضًا، ولا شيء مختلف فيه، يمكن مع ذلك الاطلاع على مثالّين سريعَين.
تمارين
ب. قم بتحويل العدد الممثل بطريقة المتمم الثنائي إلى النظام العشري:
\[10111\]جـ. قم بإجراء عملية الطرح التالية (حيث الأعداد ممثلة بطريقة المتمم الثنائي) وإعطاء الناتج بالنظام العشري:
\[10010001 - 0110\]ضرب الأعداد الثنائية
يمكن إجراء عملية الضرب في النظام الثنائي يدويًا مثل ما نجريها في النظام العشري، ولكن مع العلم أن ضرب عددين ضمن السعة N بت يتطلب ضعف السعة أي 2N . لاحتواء كل القيم الناتجة الممكنة. لذا، يمكن مضاعفة المساحة مباشرة للعددين الذين يستخدمان طريقة المتمم الثنائي، ثم إجراء الضرب بشكل عادي (مع تجاهل أي تجاوز في السعة الجديدة).
فمثًلا إذا كان لدينا العددين 6 و -5 ضمن مساحة 4 بت، فإن ناتج ضربهما (-30) لا يتسع في 4 بت ويتطلب 8 بت، لذا يمكن مضاعفة المساحة قبل إجراء الضرب، ثم القيام بعملية الضرب، كما في المثال أدناه (وُضعت علامة x لتجاهل البتات المتجاوزة للسعة المعطاة وهي 8 بت):
ولكن هذه الطريقة غير فعالة، فبمضاعفة المساحة المحددة قبل الضرب نكون قد ضاعفنا عمليات الضرب الجزئية اللازمة وكذلك عمليات الجمع التي تتبعها.
تطبق الحواسيب خوارزميات مختلفة أكثر فاعلية لإجراء عملية الضرب، وبالأخص مع استخدام طريقة المتمم الثنائي لتمثيل الأعداد السالبة، مثل خوارزمية Booth’s multiplication algorithm بالإضافة لخوارزميات أخرى، والتي لن أخوض في تفاصيلها هنا لعدم الإطالة والتعقيد. وأترك لك مهمة البحث والاطلاع على تلك الخوارزميات.
تقسيم الأعداد الثنائية
لا شيء مميز في تقسيم الأعداد الثنائية عما هو عليه في الأعداد العشرية. ويمكن أخذ مثال سريعًا:
للاطلاع: ما الذي يحدث إذا جربنا التقسيم على صفر في الحاسوب الميكانيكي Friden STW10؟ https://www.youtube.com/watch?v=7Kd3R_RlXgc
الإزاحة Shifting
لنتحدث عن مفهوم الإزاحة وكيفية تمثيل الفاصلة العشرية في الحاسوب في الفقرة التالية: نعلم أننا عندما نضرب عدد ما في النظام العشري بمضاعفات العدد عشرة، أي بـ \(10^k\) ، فإننا نُزيح العدد إلى اليسار بمقدار k خانة، فمثلًا عند ضرب العدد 5 بـ 10 نُزيح العدد 5 خانة واحدة إلى اليسار، ونضع مكان الفراغ الناتج صفرًا فيصبح 50..وعند ضربه بـ 100 نزيح العدد 5 خانتين لليسار ونضع مكان الفراغين الناتجين أصفارا أي 500 وهكذا..
أعلمُ أنك درست ذلك في المدرسة على أنه إضافة أصفار لليمين، ولكنني أريدك هنا أن تفكر بالأمر وفق هندسة الحاسوب على أنه إزاحة العدد نحو اليسار ووضع أصفار مكان الفراغات الناتجة..فهذه هي الطريقة المتعامل بها في الحاسوب.
وكذلك عند التقسيم على \(10^k\) فإننا نزيح العدد نحو اليمين بمقدار k خانة.
والآن نفس الشيء يحدث في النظام الثنائي. فعندما نضرب عددًا ما في النظام الثنائي بمضاعفات العدد 2، أي \(2^k\) ، فإننا نُزيح العدد نحو اليسار بمقدار k خانة، في المثال هنا قمنا بالضرب بـ \(2^2\) لذا أزحنا العدد خانتين نحو اليسار.
\[\textcolor{blue}{1101} × 100 = \textcolor{blue}{1101}00\]كذلك إذا قسمنا عدد ثنائي على \(2^k\) فإننا نزيح العدد مقدار k خانة نحو اليمين.
ويمكن تفسير ذلك في النظام العشري على أنه تقسيم 26 على 4 فيكون الناتج 6 والباقي 2.
يمكن عند ضرب عدد ثنائي بمضاعفات العدد 2، أي بـ \(2^k\) ، إزاحة العدد نحو اليسار بعدد خانات k، تمامًا مثلما نزيح العدد في النظام العشري عند الضرب بـ \(10^k\) . مثال (في النظام الثنائي):
\[1101 × 100 = 110100\]لاحظ كيف أزحنا العدد 1101 مرتبتين لليسار، ووضعنا مكان تلك المرتبتين أصفارًا.
كذلك إذا قسمنا عدد ثنائي على \(2^k\) فنزيح العدد مقدار k مرتبة نحو اليمين.
مثال: تقسيم 26 على 4 يعطي 6 والباقي 2، ويكون هذا في النظام الثنائي (لاحظ أن 4 من مضاعفات العدد 2 وهي \(2^2\) وبالتالي يمكن تطبيق الإزاحة):
لقد تحدثنا في فقرة سابقة عن الـ Carry bit. ويتم استخدامه هنا أيضًا لحفظ الباقي.
والآن، لنعد قليلًا للأعداد ذات الفاصلة، تلك الفاصلة نسميها عادة الفاصلة العشرية (decimal point)، ولكن كوننا علمنا أنه يوجد أنظمة عد أخرى، وأن الفاصلة ليست مرتبطة بالنظام العشري فقط، فلنمسيها الفاصلة فقط (وبالإنجليزية radix point).
وقد قلنا أنه لا يمكننا تعريف الأعداد السالبة في الحاسوب بوضع إشارة السالب (-). وبنفس المبدأ، لا يمكن تعريف الأعداد ذات الفاصلة بوضع فاصلة، بل يجب إيجاد طريقة لتمثيل تلك الفاصلة في الحاسوب. فكيف يمكن ذلك؟
هنا، قام الأشخاص المعنيون بالتفكير نيابة عن البشرية بالتفكير في الأمر!، وتوصلوا إلى أنه يمكن تمثيل كل الأعداد التي تحوي فاصلة بشكل موحد وفق الشكل التالي: بحيث يكون لدينا رقم واحد فقط قبل الفاصلة، أي بالشكل التالي وفق النظام العشري:
\[562,5 = 5,625 × 10^2\]حيث قمنا بتحويل العدد من الشكل 562,5 إلى الشكل الموحد عبر إزاحة الفاصلة حتى نحصل على رقم واحد قبلها، ثم نضرب بعشرة أس مقدار الإزاحة.
وكما أننا نضرب بـ 10 في النظام العشري، نضرب بـ 2 في النظام الثنائي كما نعلم:
\[101,101 = 1,01101 × 2^2 = 5,625_{10}\]وبما أننا نضرب دائمًا بـ 2 في النظام الثنائي، فالرقم 2 هو ثابت ولا داعي لحفظه في الذاكرة، بل يكفي حفظ الأس الخاص به والذي يعبر عن مقدار إزاحة الفاصلة للوصول للشكل المطلوب.
وكذلك نعلم أن كل الأعداد في النظام الثنائي ستكون واحد فاصلة كذا، أي سيكون الرقم قبل الفاصلة دائمًا واحد، ﻷن الصفر على اليسار ليس له قيمة كما نعلم..ولكن لحظة..قد يعبر الصفر على اليسار عن العدد الموجب (بت الإشارة). نعم صحيح، لذا تم تقسيم الذاكرة الخاصة بحفظ الأعداد ذات الفاصلة لثلاث أقسام:
- قسم مؤلف من بت واحد وهو بت الإشارة Sign واختصارا S
- قسم لوضع الأس الخاص بالرقم 2، ويسمى Exponent
- قسم لوضع العدد بعد الفاصلة، ويسمى Mantissa (وهي كلمة لاتينية تعني “القيمة الثانوية” أو ماشابه).
فإذا أردنا حفظ العدد الذي ذكرناه، وبما أن العدد موجبًا كما رأيناه في النظام العشري، فنضع 0 مكان بت الإشارة، ثم لدينا الأس 2 ( \(2^2\) ) أي 10 في النظام الثنائي (ولكن لا يتم حفظه بهذا الشكل، نعم اصبر قليلا)، ولدينا العدد 01101 بعد الفاصلة:
تسمى هذه الطريقة بـ implicit normalization of floating point numbers. حيث يكون لدينا 1 دائمًا قبل الفاصلة، ولهذا سميت implicit ﻷن الواحد هذا مضمّن (أي مفهوم ضمنًا) ولا يتم حفظه في الذاكرة بشكل صريح لتوفير المساحة.
تعمل بالمقابل طريقة الـ explicit أي الصريحة بإزاحة الفاصلة ليسار العدد بالكامل، لينتج لدينا صفر فاصلة العدد الذي لدينا:
\[101,101 = 0,101101 × 2^3\]أي يكون على يسار الفاصلة صفر دائمًا، وبهذا نضطر لتخزين ذلك الواحد (المضمن في الطريقة الأولى) في قسم الـ Mantissa، وبالتالي تأخذ هذه الطريقة بت واحد إضافي عن الطريقة implicit، لذلك تعتبر الطريقة التي تعلمناها بدايةً (implicit) أفضل.
والآن لنعد للأس Exponent والذي لم نحفظه 10 كما ذكرنا! فلماذا؟
ﻷننا نريد تمثيل الأعداد الطويلة (الكبيرة جدا أو الصغيرة جدا)، أو بالأحرى أطول عدد ممكن، فلو كان لدينا مثلًا العدد:
\[0,0001001101 = 1,001101 × 2^{-4}\]لاحظ أن الـ exponent هنا أي الأس أصبح سالبًا (-4). ﻷن العدد هنا صغير جدًا وأزحنا الفاصلة نحو اليمين بدلًا من اليسار (حيث تزاح الفاصلة لتصبح يمين أول 1، ليكون لدينا دائمًا الرقم 1 قبل الفاصلة). لذا يجب التفكير بطريقة لتمثيل الأس السالب والموجب معًا. هنا تقول لي: إي بسيطة..نستخدم المتمم الثنائي، فهو موضوع أصلًا لتمثيل الأعداد السالبة والموجبة معًا. ﻷجيبك بأننا لا نستخدمه هنا! ولكن ما السبب؟
نريد في تمثيل الأس الميزة التالية: إمكانية مقارنة عددين مع بعضهما بتًا بتًا (bit by bit). وﻷن طريقة المتتم الثنائي لاتعطي الأعداد بالترتيب كما تعلمنا (انظر مجددا للجدول 20) فلا يتم استخدامها هنا. كذلك إذا استخدمنا البت الأول للإشارة فلن نتمكن من مقارنة عددان على مستوى الـ bits أي بتًا تلو الآخر. ألم تفهم تمامًا؟ لنأخذ مثال:
لنستخدم في البداية طريقة المتمم الثنائي في كتابة الأس، ونكتب عددين بهذه الطريقة لنرى كيف يمكن أن نقارنهما مع بعضهما (لا تنس أننا ما زلنا نستخدم طريقة التمثيل التي تعلمناها للتو، البت الأول للإشارة، ثم أربع خانات للأس ثم خمس خانات لما بعد الفاصلة، وطريقة المتمم الثنائي نستخدمها هنا لتمثيل الأس):
حيث نضع أولا بت الإشارة ثم بتات الأس ثم ال Mantissa أي مابعد الفاصلة
نعلم من التمثيل العشري المعطى للأعداد أن العدد الأول أكبر من الثاني، ولكن الحاسوب لا يرى سوى التمثيل الثنائي، ويصعب علينا المقارنة وفقا للتمثيل الثنائي بهذه الطريقة، فلإجراء المقارنة يجب أن نحسب العدد الأول بأخذ الـ Mantissa وضربها بـ 2 مرفوعة للأس المعطى أي:
\[01101 × 2^2\]ونحسب نفس الشيء للعدد الثاني أي:
\[01110 × 2^{-2}\]ونقارن الناتجين.
\[1,01101 × 2^2 = 101,101\] \[1,0111 × 2^{-2} = 0,010111\]كما ترى فالعملية صعبة ومعقدة على الحاسوب كذلك. ولكن ما البديل؟
البديل هو ما يسمى biased exponent ويتم حسابه وفق التالي: يجب أولًا معرفة المساحة المخصصة للأس (exponent) وفي حالتنا هذه في المثال أعلاه، فقد تم تخصيص 4 بت، ونعلم أن الأس يمكن أن يكون سالبًا أو موجبًا، لذا يمكن لـ 4 بت أن تتسع للأعداد من -8 إلى 7. والآن نحسب الـ Bias عبر تجاهل الإشارة هنا، حيث نأخذ أكبر عدد يمكن تمثيله بغض النظر عن الإشارة، لنجد أنه 8، إذًا الـ Bias هو 8 في هذه الحالة (أي في حالة 4 بت) والآن يمكن حساب الـ biased exponent بجمع الأس الذي لدينا مع الـ Bias، وبالتالي بدلًا من 2 يصبح 2+8 ويساوي \(10_{dec}\) أي \(1010_{bin}\) . وكما ذكرنا، لا نستخدم الإشارة هنا، أي أن الواحد الأولى على اليسار لا تعبر عن إشارة العدد بل هي جزء منه.
إذا نظرنا لما جرى عند إضافة 8 لكل أس محتمل، فسنجد أن المجال تغير ليصبح من 0 لـ 15:
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 | -1 | -2 | -3 | -4 | -5 | -6 | -7 | -8 | exponent |
| 15 | 14 | 13 | 12 | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 | Biased exponent (for 4 bit: +8) |
والآن هل تُحسِّن هذه الطريقة من عملية المقارنة؟ لنرى كيف أصبح العددين أعلاه:
\[0 \quad 1010 \quad 01101 = 5,625_{dec}\] \[0 \quad 0110 \quad 01110 = 0,359375_{bin}\]والآن أصبحت المقارنة سهلة جدا! حيث يمكن معاملة كل عدد أعلاه بالكامل على أنه عدد واحد صحيح (integer) فيكون العدد الأول 0101001101 والثاني 0011001110 ومن السهل جدًا رؤية أن العدد الأول وفق هذا التمثيل أكبر من الثاني (الرقم الثاني من اليسار 1 في العدد الأول و 0 في العدد الثاني)، ويمكن للحاسوب إجراء المقارنة بتًا تلو الآخر ليجد ذلك بسهولة أيضًا.
ولكن كيف يمكن الآن إجراء العملية العكسية؟ أي كيف نُرجع العدد من التمثيل هذا إلى الأصل؟
باستخدام القانون البسيط التالي:
\[(-1)^S × 1,M × 2^{(E - Bias)}\]أي -1 مرفوعة لبت الإشارة (S من Sign bit)، فإذا كان بت الإشارة 1 يبقى العدد -1 أي سالب، وإذا كان بت الإشارة 0 فأي عدد أس صفر يُعطي +1. ثم 1 فاصلة الـ Mantissa وهو العدد كما هو بعد الفاصلة، ثم لتحديد موضع الفاصلة الصحيح نضرب بـ 2 مرفوعًا لأس التمثيل الذي لدينا في الـ Exponent ويكون biased exponent مطروحًا منه الـ bias.
لنأخذ الآن مثالًا آخرًا على تحويل عددًا ذو فاصلة للتمثيل الذي تعلمناه.
تمرين
قم بتحويل العدد \(0.00110_{10}\) للتمثيل implicit normalization بوجود مساحة 4 بت للأس (Exponent) و 5 بت لما بعد الفاصلة (Mantissa).
الحل:
في البداية نزيح الفاصلة ليصبح لدينا الرقم 1 قبل الفاصلة:
\[0,00110 = 1,10 × 2^{-3}\]لدينا مساحة 4 للـ exponent وبالتالي فإن أكبر عدد يمكن تمثيله بغض النظر عن الإشارة هو:
\[2^{N-1} = 2^{4-1} = 2^3 = 8\]وهو الـ Bias، ولدينا الأس -3 وبالتالي يكون الـ biased exponent:
والعدد موجب أي أن بت الإشارة 0 فيكون التمثيل النهائي:
\[0 \quad 0101 \quad 10000\]حيث نملأ الـ Mantissa من اليسار لليمين وإذا زاد مساحة نضع أصفارا. لنجرب التحويل للعدد الأصلي:
نحول في البداية الـ biased exponent وهو 0101 من النظام الثنائي للعشري فيكون 5 ونعوض في القانون:
وهو العدد المعطى في البداية بالفعل.
والآن قد تقول: أرى في مثالنا أن 4 بت مخصصة للأس و5 للعدد بعد الفاصلة، هل التخصيص دائمًا كذلك؟
طبعًا لا، عدد البتات المخصصة يتبع للمعيار المستخدم، والمعيار الأكثر شيوعًا يسمى IEEE 754، وهو ما سنتحدث عنه في الفقرة القادمة.
معيار IEEE 754 لتمثيل الأعداد ذات الفاصلة
معيار IEEE 754 هو عبارة عن مجموعة قواعد لتحديد وتوحيد طريقة تمثيل الأعداد ذات الفاصلة في الحواسيب وطرق التعامل معها وقواعد التقريب الخاصة بها. وُضعت هذه القواعد بداية في عام 1985 وتمت مراجعتها وتحديثها عام 2008 ومرة أخرى عام 2019. ويحوي هذا المعيار بداخله عدة معايير بناء على المساحة المعطاة لتمثيل الأعداد ذات الفاصلة، حيث يوجد مثلا معيار binary16 حيث يتم تخصيص 16 بت بالمجمل (مساحة كل الأقسام المذكورة سابقا مجتمعة) ويسمى هذا المعيار أيضًا half precision أي نصف الدقة، حيث تعبر الدقة عن عدد الأرقام بعد الفاصلة، وكلما زاد ذلك العدد زادت الدقة الحسابية. والمعيار الثاني والذي سندرسه هنا سريعًا هو binary32 أو Single precision حيث يتم تخصيص 32 بت بالمجمل، 1 للإشارة و8 للـ exponent و 23 لما بعد الفاصلة (Mantissa). طريقة التمثيل في معيار IEEE 754 عمومًا وحساب الـ biased exponent هو نفس ما ذكرته لك سابقًا، ولكن الـ Bias فقط يختلف، فهو ليس \(2^{N-1}\) وإنما \(2^{N-1} -1\) . أي في حالتنا هنا حيث لدينا 8 بت للـ exponent فيكون الـ Bias هو 27 – 1 أي 127.
ولكن لماذا يكون هنا أقل بواحد؟ السبب هو أن المعيار هذا يخصص العدد \(0_{10}\) أي الذي يكون كله أصفار في النظام الثنائي وكذلك العدد \(255_{10}\) أي الذي يكون كله واحدات في النظام الثنائي، للدلالة على تمثيلات مختلفة وبحسب الـ Mantissa في كل حالة، إذا كانت كلها أصفار كذلك أم غير ذلك. سنرى ذلك بالتفصيل بعد مثال سريع.
مثال: قم بتحويل العدد \(116_{10}\) للنظام الثنائي ثم تمثيله بصيغة IEEE 754 Single Precision. الحل: في البداية، نستخدم للتحويل إما طريقة التقسيم على 2 التي تعلمناها أو الطريقة الأسرع وهي معرفة أكبر أس للعدد 2 والذي يمثل العدد المعطى 116 أو عددا أقل منه. نجد أن \(2^6\) يساوي 64 وهو أكبر أس يمكن أن يمثل هذا الرقم وبالتالي سيحوي التمثيل الثنائي 7 خانات فقط. ثم نحتاج لـ \(2^5\) أي 32 ليصبح المجموع 96 وبقي 20. وهو \(2^4\) أي 16 و \(2^2\) . وبالتالي:
| $2^0$ | $2^1$ | $2^2$ | $2^3$ | $2^4$ | $2^5$ | $2^6$ |
| 0 | 0 | 1 | 0 | 1 | 1 | 1 |
والآن لنقم بتمثيل العدد الناتج 1110100 بالصيغة المطلوبة. لنقم بتحويله لعدد ذو فاصلة وفق implicit normalization:
\[1110100 = 1.110100 × 2^6\]لنحسب الآن الـ biased exponent، فقد علمنا أن Single Precision يحوي 32 بت 8 منها مخصص للـ exponent وعلمنا أنه يوجد تمثيل خاص لذا يكون الـ bias بالشكل \(2^{N-1}-1\) أي 127، الأس الذي نتج لدينا أعلاه في العدد هو 6 (المرفوع للرقم 2) لنقم بجمعه مع 127:
biased exponent = 6 + 127 = 133
والآن بقي تحويل 133 للعد الثنائي وانتهى الأمر. ومثلما قمنا بتحويل 116 سابقا، ولكن هذا المرة يمكن استخدام \(2^7\) أي 128 ويبقى 5 أي \(2^2\) و \(2^0\) :
| $2^0$ | $2^1$ | $2^2$ | $2^3$ | $2^4$ | $2^5$ | $2^6$ | $2^7$ |
| 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 |
لنقم أخيرا بملء الخانات المخصصة، حيث نعلم أن العدد المعطى موجب أي بت الإشارة 0 :
| $110100 \quad 00000000000000000$ | $1000 \quad 0101$ | 0 |
وكما تعلم، في حال كان ال biased exponent لدينا أقل من 8 خانات نضيف أصفار على اليسار، أما في الـ mantissa أي العدد بعد الفاصلة فنضيف أصفار على اليمين.
والآن ما هي القيم التي يخصصها المعيار IEEE 754؟ إليك الجدول التالي والذي يشمل كل القيم الممكنة في هذا المعيار، حيث ينتج التمثيل الخاص عند اجتماع القيم المحددة للـ exponent والـ Mantissa (العدد بعد الفاصلة).
| القيمة الممثلة | MANTISSA | EXPONENT |
|---|---|---|
| 0 | 0 | 0 |
| Infinity ∞ | 0 | 255 |
| Implicit Normalized Form | not 0 | not 0 |
| Fractional Form | not 0 | 0 |
| Not a number (NAN) | not 0 | 255 |
ولكن ما معنى القيمة الأخيرة NAN؟ يتم تخصيص هذه القيمة واستخدامها في البرمجة للدلالة على العدد غير المعرف، وهو ما يحدث في اﻷخطاء الحسابية، مثلا عندما يتم التقسيم على صفر، أو جذر عدد سالب.
والسطر الثالث هو القيمة التي تمثل عمومًا، أي التي تمثل أي عدد ذو فاصلة. أما السطر الرابع فنفس الشيء ولكن يكون الرقم قبل الفاصلة صفرًا، وهو ناتج أي عدد كسري مثل ¼ أي 0.25 أو ½ أي 0.5 وما إلى ذلك.
مثال 2: لديك التمثيل التالي بصيغة IEEE 754 Single Precision.
| $110000 \quad 00000000000000000$ | $1000 \quad 0011$ | 0 |
والمطلوب إيجاد العدد العشري الذي يمثله ذلك. الحل: نعلم من بت الإشارة أن العدد موجب. لنقم بتحويل الـ biased exponent لعدد عشري، حيث لدينا واحد أقصى اليسار والذي يمثل \(2^7\) أي 128 ثم لدينا في الآخر واحدان يعبران عن الرقمين 2 و 1 وبالتالي يكون العدد 128+2+1 ويساوي 131. نطرح منه الـ bias فيكون
\[131 – 127 = 4\]وبتطبيق القانون:
\[(-1)^S × 1,M × 2^{E – 127} = 1,11 × 2^4 = 11100\]حيث أزحنا الفاصلة أربع خانات نحو اليمين بناء على الأس 4. بقي تحويل العدد 11100 من الثنائي للعشري. نلاحظ أنه مؤلف من 5 خانات وبالتالي الواحد على اليسار تمثل \(2^4\) يليها \(2^3\) يليها \(2^2\) وهذا يكون 16+8+4 وينتج 28. انتهى
إذا تابعت معي جيدًا ما تعلمناه إلى الآن، ستلاحظ أنه أًصبح لدينا طريقتان لتمثيل الأعداد السالبة، وهما المتمم الثنائي والـ biased exponent. وبالتالي لماذا لا نعتمد على الأخيرة مثلا بشكل دائم لتمثيل الأعداد السالبة ونستغني عن المتمم الثنائي؟
يبدو أن ذلك ممكنا، ولكن الجواب هو مزايا وعيوب كل واحدة، فصحيح أن المقارنة كما ذكرنا تكون سهلة في الـ biased exponent، إلا أنه يتطلب خطوة إضافية للتحويل للقيمة الأصلية. بينما يتيح المتمم الثنائي إجراء العمليات الحسابية بشكل مباشر.
وبهذا نكون قد انتهينا بفضل الله من التعرف على أنظمة العد وتمثيل الأعداد في الحاسوب وفق نظام العد الثنائي، والعمليات الحسابية عليه وتمثيل الأعداد السالبة والموجبة وذات الفاصلة.
وقد علمنا أن الحاسوب يعمل بنظام العد الثنائي المؤلف من 0 (انعدام تيار في السلك) و 1 (وجود تيار) ولا يمكنه التعامل سوى مع الأصفار والواحدات بطريقة التيار تلك..ولكن يبقى ذلك غير مفهومًا تمامًا بالنسبة لك أليس كذلك؟ يعني أنت الآن تقرأ نص من الحاسوب، وترى صورًا وتشاهد مقاطع فيديو، فكيف يتم تمثيل هذه النصوص والصور والأصوات والمقاطع بالأصفار والواحدات؟ هذا ما سنتعلمه في المقال القادم إن شاء الله.
تمرين
د. قم بتحويل العدد 132 للنظام الثنائي ثم تمثيله بصيغة IEEE 754 Single Precision.
حلول التمارين
أ. 1001
ب. -9
جـ. -117
د. 01000011000001000000000000000000
لتمارين أكثر، يمكنك الاطلاع على المقال: أمثلة في أنظمة العد